$\longrightarrow\(Lors d'un mouvement il ya toujours conservation de l'énergie

Définitions

Energie Cinétique
Forces conservatives et énergie potentielle
Energie mécanique

Etude graphique du mouvement d'un système conservatif

On considère un point matériel soumis à des forces conservatives. Le point va explorer un espace où existe une énergie potentielle.
\)\to\(On se propose de lacher un point matériel en un point M et suivre son évolution: Quelle sera son mouvement ultérieur? >2 règles:
>- \)E_m=cst\(
>- \){{E_c=\frac 12mv^2}}\geq 0\implies E_m-E_p\geq0\(
>\)\implies E_m\geq E_p\quad\text{ou}\quad {{E_p\leq E_m}}\(

Exemples

Exemple 1: Chute libre d'un point matériel
\)\to\( Absence des frottements

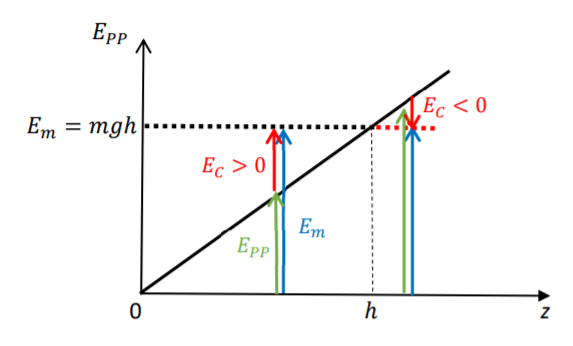
La partie rouge correspond à un mouvement impossible car l'énergie cinétique est négative
Exemple 2: Cas général

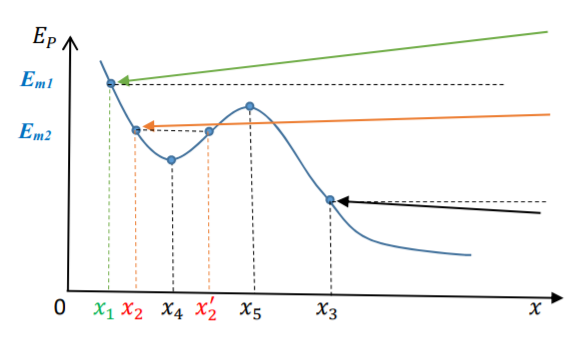
Vert \)\to\( état libre car \)E_{m1}\( n'est jamais égalée quand PM est laché en \)x_1\(
Orange \)\to\( état lié car \)E_{m2}\( est égalée quand PM est laché en \)x_2\( \)\implies\( oscillation
Noir \)\to\( état libre
Equilibre stable / instable: \)x_4\( et \)x_5\( sont des positions d'équilibres \)\iff {{E_p}}\( extremale

• \)x_4\(: Stable
• \)x_5\(: Instable

Position d'équilibre stable / instable:

\)$\vec F=-\overrightarrow{grad}E_p=-\frac{dE_p}{dx}\vec e_x={{0}}\quad \text{ à la position d'équilibre}$$
\(\longrightarrow\) Le maximum et minimum de l'énergie potentiel correspondent aux position d'équilibres

• Position stable: \(\frac{d^2E_p}{dx^2}{{\gt 0}}\implies \text{convexe}\)
• Position instable: \(\frac{d^2E_p}{dx^2}{{\lt 0}}\implies \text{concave}\) \(\implies\) légère perturbation, la position d'équilibre ne reviendra plus